In this lesson you will learn:
In Lesson 4 we learned a lot about economics just from studying Robinson Crusoe and his “exchanges” with Nature. However, the true meat of economics comes from studying trades involving more than one person. To understand a market economy we need to first understand individual trades between two people, because individual trades are the building blocks of the entire market economy.
For Robinson Crusoe, every “exchange” that he made with Nature was designed to benefit himself. Crusoe only chose those alternatives where he judged that the benefits outweighed the costs.
The same is true when a person exchanges, not with Nature, but with another person. Since we are assuming (in Part II of this book) a market economy with secure property rights, we know that both people in a voluntary exchange expect the benefits of the trade to outweigh the costs. In other words, both parties expect to walk away from the trade better off than they were before the trade.
How can this be possible? Some critics of capitalism think that if one person gains from a trade, it must be at the expense of the other party; they believe that one man’s gain translates into another man’s loss. But these critics are wrong! Remember that preferences are subjective. Suppose Tina comes to school with an orange in her lunch, and Sam comes to school with an apple. It wouldn’t be strange if Tina would prefer an apple to her orange, while at the same time Sam would prefer an orange to his apple. If Sam and Tina become aware of each other’s predicament, they can both be happier by trading.
Very often people make mistakes in their forecasts of what will make them happy. For example, maybe Sam has too much acid in his system and eating the orange causes a burning sensation, so that he ends up throwing it out after two bites. In that case, Sam will regret that he made the earlier trade with Tina. Even so, the important point for now is that at the moment of exchange, both parties in a voluntary trade (expect to) benefit from it. So long as the exchanges are voluntary and honest—in other words, so long as the exchanges aren’t forced or based on deception—people can achieve more of their goals by having the option of trading their property with each other.
Ultimately we want to explain exchanges involving money. For most readers, this will mean explaining the prices of goods and services as they are traded against dollars, euros, yen, and so forth. We will actually explain these principles in the next lesson. For the remainder of this lesson, we will explain the principles behind exchanges that do not involve money. Specifically, we will focus on (what economists call) direct exchange, or what is also called barter.
In a direct exchange, both parties have a “direct” use for the object that they are receiving in the trade. Our story of Tina and Sam involved direct exchange, because each student wanted the other’s fruit in order to consume it.
Direct exchange (or barter) can involve not only consumption goods, but also producer goods. (Refer back to Lesson 4 if you don’t remember the difference.) For example, Farmer Brown might give a pound of bacon to Farmer Jones, in exchange for a bag of tomato seeds. Farmer Jones values the bacon as a consumption good; he will fry it and eat it that morning for breakfast. But Farmer Brown doesn’t want to eat the tomato seeds he got in exchange! No, they are a producer good for him, because he will mix them with other items (such as soil and fertilizer) in order to produce tomatoes in the future. Don’t be confused: Even though you might say that Farmer Brown doesn’t “directly” benefit from the tomato seeds, the trade still counts as “direct exchange” (or barter) because both farmers want to personally use the items they receive in the transaction.
We only leave a state of barter and enter the realm of indirect exchange when people receive an item during a trade that they don’t plan on using themselves, whether for consumption or production. What happens in this case is that they plan on trading the item away to somebody else in the future. This is actually what happens in every trade involving money. When you sell a few hours of your leisure cutting your neighbor’s lawn for $20, you are engaged in indirect exchange. You don’t plan on eating the $20 bill, and you don’t intend to combine it with other materials in order to build something. The reason you value it, is that you expect to be able to find somebody else (in the future) who will sell you something you do directly value, in exchange for the money. We will develop the theory of indirect exchange in the next lesson. Here, we are explaining direct exchange (or barter), where both parties intend to use the traded objects for consumption or production (but not for a subsequent exchange).
In any market exchange, units of one good (or service) are traded for units of another good (or service). The price is the ratio of those units. For example, if the price of a DVD is $20, that means the buyer must give up 20 units of dollars while the seller gives up one unit of the DVD.
In barter, the familiar distinction between buyer and seller disappears, because there is no money. For example, when Farmer Brown gives a pound of bacon to Farmer Jones in exchange for (say) 100 tomato seeds, Brown is simultaneously a buyer of seeds and a seller of bacon. (Of course, Jones is the opposite: a buyer of bacon and a seller of seeds.) We can also say that the price of a pound of bacon is 100 tomato seeds, and that the price of a tomato seed is 1/100 of a pound of bacon.
As we will see in the next lesson, part of the beauty of a monetary economy is that we don’t need to use barter prices, with every good (and service) having an entire list of exchange rates with every other good (and service) in the economy. For example, if there are 20 different types of goods that all trade against each other, then a trader in a pure barter economy would (in principle) need to keep track of (20x19)/2=190 different exchange ratios, or barter prices. But if there is one type of good involved in every trade—and that’s precisely what money does—then the trader only needs to keep track of 20 prices: the exchange rate of each of the 20 goods against units of money. But before we can explore (in the next lesson) the special case of how prices are formed when money is involved in every transaction, we need to first understand the more general case of barter. We explore this topic in the next section.
For the remainder of this lesson, we will work with a specific numerical example to illustrate why specific prices occur in barter exchanges. Of course there is nothing magical about the numbers we will choose; the idea is simply to give you a concrete example to make sure you can visualize the more general principles.1
Our example revolves around three siblings—Alice, Billy, and Christy— who arrive home on Halloween after an evening of Trick or Treating. They each start with different amounts of Snickers and Milky Way candy bars. As we will see, because of their different holdings, and because of their different tastes, the children will be able to reap gains from trade. In other words, through voluntary exchanges, the children will all walk away from their small “market” happier than they entered it. In our hypothetical example, we want to ultimately show why a specific exchange rate between Snickers and Milky Ways emerges. In other words, we want to understand how the children’s initial holdings and their preferences will lead to a specific “Snickers-price” of Milky Ways, or (equivalently) a specific “Milky-Way-price” of Snickers.
In order to work through the example, we’ll first need to come up with a convenient way to represent the information. The following table represents Alice’s preferences, or rankings, of various combinations of Snickers and Milky Way bars. To keep things manageable, we will only consider cases where the children can have at most four of each type of candy bar. That means there are 25 possible combinations each child could have, in our example. (One possibility is having 4 Snickers and 4 Milky Ways. A second possibility is having 3 Snickers and 0 Milky Ways. A third possibility is having 1 Snickers and 2 Milky Ways. And so on, for all 25 possibilities.)
Before proceeding, let’s make sure you understand the information in the table on the next page. We have chosen the numbers so that there is a definite sense in which Alice “likes Snickers more than Milky Ways.” For example, if Alice initially has no Snickers or Milky Ways, and if she has to choose just one, she will pick a Snickers. The table below tells us this, because the combination (0 Snickers, 0 Milky Ways) has the lowest ranking, while the combination (1 Snickers, 0 Milky Ways) is ranked at 23rd, above the combination (0 Snickers, 1 Milky Ways) which is ranked in second-last place.
However, it’s important for you to remember that people value goods unit by unit (or “on the margin”). It’s true that if Alice initially has zero of each candy bar, she would prefer to receive a Snickers over a Milky Way. However, suppose that Alice already starts out with 1 Snickers bar. Now if someone offers her a choice between an (additional) Snickers versus a Milky Way, she will choose the Milky Way. This is because Alice ranks the combination (1 Snickers, 1 Milky Way) in 17th place, which is well above the combination (2 Snickers, 0 Milky Way) coming in at a lowly 21st place.
We have constructed Alice’s ranking to be systematic; she basically likes Snickers more than Milky Ways, and she also prefers to have more candy rather than less. But notice that Alice also prefers variety. For example, she would rather have 1 Snickers and 1 Milky Way—ranked in 17th place—than 3 Snickers and 0 Milky Ways (ranked in 19th place). In this specific comparison, at first glance it seems that Alice is violating two of the “rules” of her tastes—she is opting for fewer candy bars and fewer Snickers bars! But there is nothing strange going on here at all. The 17th-ranked combination gives her an even mixture of Snickers and Milky Ways, whereas the 19th-place combination, even though it has an extra candy bar, is loaded up with all Snickers. So there is nothing odd or “irrational” about Alice preferring the combination of 1 bar of each. Just as we can’t say that people value water more than diamonds, by the same token we can’t really say that Alice values Snickers (or more candy bars) more than she values Milky Ways (or fewer candy bars). It all depends on how many units of each good Alice starts out with when she is faced with a specific decision.
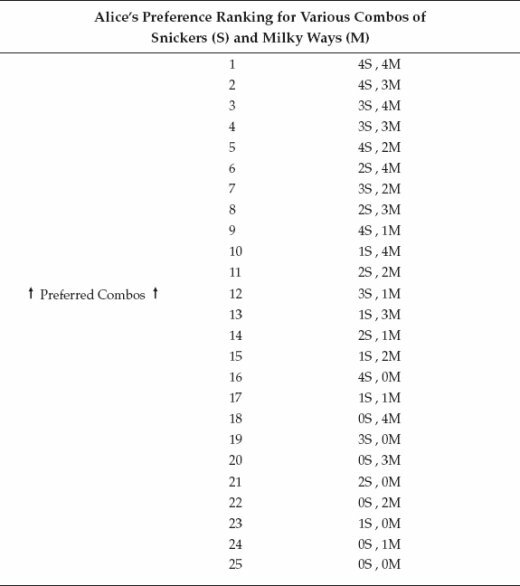
If you spend a few moments studying the table above, you will see the patterns in her preferences. In the real world, people’s preferences don’t mechanically obey a simple set of “rules,” but we picked the commonsense ranking above to make it easier for you to follow the example.
Now that we understand Alice and her preferences, we can add her brother Billy to the mix. We’ll suppose that his tastes are identical to Alice’s. However, because the children start out with different combinations, there are still gains from trade. This information (and more) is summarized in the following table.
To repeat, we have purposely chosen Billy’s preference rankings to be identical to Alice’s, in order for you to see the effects of the children starting with different combinations of candy bars. In the real world, of course, people aren’t identical copies of each other, especially when their preferences can encompass not merely 25 different scenarios, but an enormous number of combinations of many different goods and services.
Although the children have the same tastes for various combinations of Snickers and Milky Way bars, they come home from Trick or Treating with different collections. Alice comes to the bargaining table with 4 Snickers and 0 Milky Ways, while her brother shows up with 0 Snickers and 4 Milky Ways. A simple inspection of their rankings reveals that there are gains from trade. In other words, by rearranging their property, Alice and Billy can both end up with a Snicker-Milky Way combination that each subjectively prefers to the combination he or she started with.
However, economic logic alone can’t tell us the exact terms on which Alice and Billy will agree to their exchange. To keep things simple, let’s assume that they won’t be splitting candy bars, so that they can only trade whole bars. Given the information in the table, what can we say about their trading?
Alice and Billy’s Possible Trades of Snickers and Milky Ways
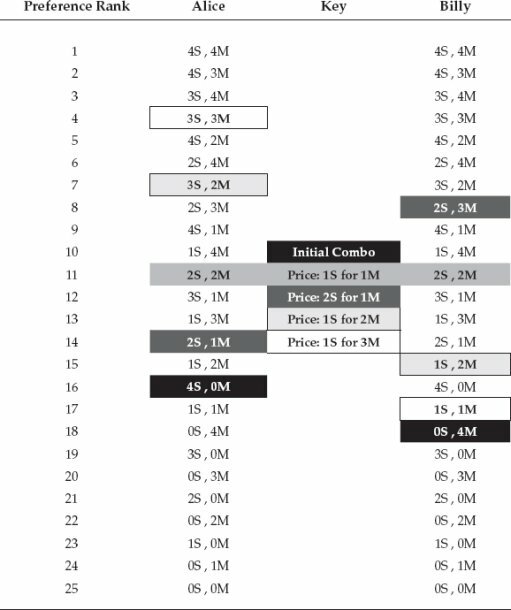
The first principle to remember is that in a voluntary trade, both parties benefit. If we assume—and this might be an unrealistic assumption!—that the siblings don’t steal each other’s candy, then we know that any exchange must make Alice and Billy better off. That means we can rule out Alice ending up with any of the combinations ranked 17th through 25th on her preferences, and we can rule out Billy ending up with a candy combination ranked 19th through 25th on his preferences. It is always an option to refrain from trading and just eat the candy they personally acquired from Trick or Treating, and so each sibling will end up at least as happy after trading as he or she was before trading.
Because our example is so simple, we can pretty quickly run through the possible trading outcomes by experimenting with various “prices.” Suppose that Alice and Billy trade Snickers for Milky Ways at the ratio of 1:1. Are there mutually advantageous trades at this price?
Let’s look at Alice’s preferences first. She starts in the 16th-ranked cell, with (4 Snickers, 0 Milky Ways). So the question is: Would Alice be willing to trade away one or more Snickers bars, in exchange for an equal number of Milky Ways? We can see that the answer is yes. She could trade away 1 Snickers for 1 Milky Way, and end up with the (3S, 1M) combination ranked in 12th place. But she could do even better still by trading another unit, and moving up to the 11th ranked combination of two of each candy bar.
A similar analysis holds for Billy. He could move from the 18th ranked combination up to the 13th by trading away 1 Milky Way for 1 Snickers. But he could do better still by trading an additional unit, and moving up to the 11th ranked outcome on his own preferences.
For our current lesson, we will not delve too deeply into the exact procedure Alice and Billy use when bartering. You can imagine Alice first giving Billy 1 Snickers in exchange for 1 of his Milky Ways, and then they pause to reevaluate. Or you can imagine Alice offering 2 Snickers right off the bat, in exchange for Billy’s 2 Milky Ways. The important point is that if we set the price at 1:1, then the only stable stopping point—the only equilibrium position—occurs when Alice and Billy have rearranged their candy bars so that they both end up holding 2 of each kind. Alice wouldn’t give up a third Snickers to acquire yet another Milky Way, because that would move her back down to the 13th ranked combination (1S, 3M).
Be careful! It may seem as if we just “proved” that Alice and Billy will each end up with 2 of each candy bar, but we’ve only showed that this is the logical stopping point if they trade Snickers for Milky Ways at a 1:1 ratio (price). There are other prices that would still allow them to make mutually beneficial trades.
For example, suppose Alice says to Billy, “I will give you 1 of my Snickers bars if you give me 2 of your Milky Ways. That’s the only trade I am willing to make. Take it or leave it.” Is this a good deal? It’s certainly a good deal for Alice. It would allow her to end up with 3 Snickers and 2 Milky Ways, the 7th most valuable combination on her ranking.2
The trade would also make Billy better off. He would end up with 1 Snickers and 2 Milky Ways, an outcome that is ranked three slots higher than if he doesn’t trade at all. But he wouldn’t engage in the same trade a second time, because then he would be left with (2S, OM), a movement back down his preference ranking.
On the other hand, Billy could have issued a comparable ultimatum to Alice, saying that he would give up 1 of his Milky Ways in exchange for 2 of her Snickers, or else he would take his Halloween loot to his room and slam the door. If Alice believed his threat, she could improve her position by accepting the deal. The dark gray cells in the table above indicate the final combinations at a price of 2:1.
There is yet a fourth possibility. Suppose Alice is particularly cutthroat and demands 3 Milky Ways in exchange for just 1 of her Snickers. As the white cells indicate, this too is a possibility—if Billy really believed this to be the “going price,” he would improve his lot by moving from the initial 18th position to the 17th position.
You can check to see that there are no other prices that work, if we continue to assume that the children only trade whole bars for each other. Notice that even though the price ratio 1:3 works, the opposite does not: Alice would rather keep her original combination than give up 3 Snickers for 1 measly Milky Way, and so Billy could never push through such an offer.
Summing up, what have we learned? We have seen that the underlying preference rankings and initial combinations of candy bars allow us to identify four different stable resting points, or equilibrium positions. Another way of describing our results is to say that we have identified four different outcomes in which the gains from trade would be exhausted. We also pointed out that for each of these four positions, there is a different price.
Economic logic alone can’t tell us—with these specific numbers—how many candy bars Alice and Billy will have when they walk away from their trading session. We can’t say for sure whether they will trade Snickers for Milky Ways at a ratio of 1:1, 2:1, 1:2, or 1:3. The actual outcome will depend on factors beyond the simple preference rankings and initial distribution of candy.
For example, if Alice really “drives a hard bargain” and Billy is relatively meek, then it’s likely that she will push through the trade of 1 of her Snickers in exchange for 2 or 3 of Billy’s Milky Ways. On the other hand, if Alice and Billy are equally skilled in the art of negotiation, then perhaps the even split will occur.
In the real world, it’s possible that Alice and Billy make no exchanges, even if the table above correctly describes their preferences and candy holdings. Suppose Alice says, “Give me 2 Milky Ways and I’ll give you 1 Snickers bar, or else I walk.” Yet Billy thinks she is bluffing and says, “Nope, my best offer is to trade bars 1-for-1.” In this case, it’s certainly possible that Alice storms away, making good on her threat. In terms of our analysis, we would say that this isn’t an “equilibrium” outcome, because there are still gains from trade that remain to be exploited—Alice and Billy can still both be happier if they swap their property around. So take care not to wrap too much significance around the economic concept of equilibrium—in the real world, disequilibrium occurs all the time!
Collapsing the Scope of Prices By Adding More Traders
Despite the complications, the above example laid out some basic principles in understanding how prices are formed in a barter market. In this final section we’ll show that adding another trader can knock out some of the original possible prices. For this new twist, look at the table below, which reproduces the same rankings for Alice and Billy, but adds information about a third Trick or Treater, Christy:
Adding a Third Child Can Reduce the Number of Stable Outcomes

Notice that Christy’s preferences for candy bars are not the same as Alice’s and Billy’s. Like them, Christy prefers more candy to less, and she also enjoys variety, other things equal. However, in everyday language people would say that Christy “likes Snickers bars a lot more than Alice and Billy.” For example, Christy would rather have a single Snickers bar than have 4 Milky Ways! (Look at her 20th and 21st rankings.)
Of course, as someone trained in economic thinking, you know that there are situations where Christy would give up Snickers bars to obtain Milky Ways. For example, if she started with 4 Snickers, she would be willing to give up 2 of them to acquire 2 Milky Ways, as her 11th and 12th rankings demonstrate. But looking at her preference ranking compared to Alice’s or Billy’s, it is easy to see what the average person would mean by saying “Christy likes Snickers more than the others do,” or perhaps, “Christy does not like Milky Ways nearly as much as the others do.”
In the previous section we saw the various possible outcomes and barter prices with just Alice and Billy. What happens if Christy comes to the bargaining table before any deals are struck, and she’s carrying 1 Snickers bar and 4 Milky Ways?
Before starting the analysis, let’s lay the ground rules of how we’re picturing the negotiating process. To keep things as simple as possible, we’re going to look for outcomes where there is only one price for all the trades; in other words Alice can’t charge Christy more Milky Ways than she charges Billy. We are also going to rule out any trade in which one of the children would object and make a better offer to one of the parties. So when Christy enters the scene, some of the possible “equilibrium positions” we discussed earlier break down.
For example, suppose Alice and Billy are about to trade Snickers for Milky Ways at a 1:1 price ratio. If Christy had never shown up, we already determined that Alice and Billy would each end up with 2 of each type of candy bar. At the price of 1:1, Christy would love to participate. After Billy and Alice had swapped 2 Snickers for 2 Milky Ways, Christy might say, “OK great, I would like to trade up to 3 of my Milky Ways for 3 Snickers bars from either of you guys.” (These successive trades would move Christy from her original 13th ranked combination up to the 9th, 7th, and 6th ranked combinations.)
When Alice and Billy replied that they had done all the trading they wanted at the 1:1 ratio, Christy would be heartbroken. She could explain to Alice, “Why in the world did you trade away your Snickers at such a low price?! I would have gladly given you twice what Billy did.”
For the purposes of our analysis in this lesson, we are going to say that this type of situation does not form a stable outcome or equilibrium. There is a sense in which Alice and Christy would both regret the outcome, if the price ratio of 1:1 occurred and Alice and Billy traded according to the original outcome when it was just the two of them. Loosely speaking we say that Christy comes on the scene and “knocks out” the 1:1 price.
Similar reasoning “knocks out” the other (original) stable outcome where Alice offered 2 Snickers to receive 1 Milky Way. It would be crazy for Alice to trade with Billy at such a disadvantage, when Christy would make her a much better offer.
The other two price ratios “survive” the arrival of Christy. At the 1:3 price, Christy remains a bystander. She sees Alice propose 1 of her Snickers for 3 of Billy’s Milky Ways. He is tempted by the offer—it’s better than nothing—but he turns to Christy and asks, “Can you do better than Alice?” Christy answers no, she wouldn’t be willing to trade him her sole Snickers for only 2 Milky Ways. (We haven’t included it because of space constraints, but the combination [OS, 6M] would be ranked far below [1S, 4M] for Christy.) Likewise, after the swap with Billy went through, Alice might ask Christy, “I’d be willing to give up another of my Snickers for 3 of your Milky Ways,” but Christy would decline this offer too. So we see that 1:3 is still a stable or equilibrium price, but one on which Christy is content to “stay out of the market” and just eat the candy she personally collected from Trick or Treating.
The really interesting scenario is the price ratio of 1:2. Suppose Christy comes on the scene and observes that Alice is going to trade 1 Snickers for 2 of Billy’s Milky Ways. Christy could say, “I’ll take a piece of that action!” and Alice would be happy to oblige her. After the trades are complete, Alice ends up in her 6th ranked position, while Billy ends up in his 15th position and Christy in her 11th position. Once the candy bars have been rearranged in this fashion, there are no more gains from trade.
In this final scenario, the “equilibrium price” was 1 Snickers for 2 Milky Ways. At that price: (a) Alice sold 2 Snickers and bought 4 Milky Ways, (b) Billy sold 2 Milky Ways and bought 1 Snickers, and (c) Christy sold 2 Milky Ways and bought 1 Snickers. Notice that the total number of Snickers sold equals the total number bought, and the same for Milky Ways. Also notice that at the equilibrium price, every child is able to complete the trades he or she wanted.3
As with the analysis when there were just two children, here we can’t use economic logic alone to say what the resulting Snickers: Milky Way price will be. What we can say is that—with these specific numbers—Christy’s presence collapsed the possible range of prices. Intuitively, Christy showed up with a large supply of Milky Ways and a strong demand for Snickers, and that ruled out some of the possible prices where Snickers were fairly cheap (namely 1:1 and especially 2:1).
Obviously the Halloween example was unrealistic in many ways, and there were many real-world considerations that we ignored. We focused on important principles that will show up in later lessons, after we introduce money and focus on Supply and Demand in markets. Generally speaking, in a large market with many buyers and sellers, there is a very narrow range of potential prices that are stable in the sense we’ve discussed above. For simplicity we will normally just talk of “the” equilibrium price, as determined by the preferences and initial property holdings of all the traders in the market. We went through the Halloween story in the present lesson to show you the basic foundation on which the more standard presentation—with supply and demand curves measuring prices in dollars—is based.
